Areas of Interest
My academic interests fall under the following relatively broad categories:
- Theoretical and Applied Mechanics, Materials Physics
- Applied Mathematics, Numerical Methods
- High Performance Computing
Current Research
Parts of the following have been deliberately written in a rather chatty style. The aim was to allow people who haven't been exposed to this sort of thing to be able to read this. I have based it on the general style I used for one of my better talks. In fact, bits of this were typed as I was staring at corresponding slides. Portions of this page are currently rather incomplete, but will be populated as soon as I can make the time.
People interested in the details can of course read the linked papers, or contact me for further fascinating information. If you'd like to rush to the pretty results videos, feel free to bypass all this verbosity. I won't mind.
Development of biological tissue
The processes involved in development of biological tissue, though complex and involving several cascades of biochemical reactions, have been generally broken down into the following processes in biomechanics literature.
- Growth/Resorption
Growth (and conversely resorption) can be thought of as an addition of mass to (or loss of mass from) the various species making up the system. Densification of bone, for example. - Remodelling
Remodelling is the process of microstructural reconfiguration within a tissue. It can be viewed as evolution of the reference configuration to a remodelled configuration. An example of this is the alignment of trabeculae in bones to axis of external loading. - Morphogensis
Morphogensis involves complex changes in macroscopic form. A canonical example of this being the development of an embryo from a fertilized egg.
While these processes generally occur simultaneously during tissue development, they are viewed as mathematically independent processes for the purposes of this work.
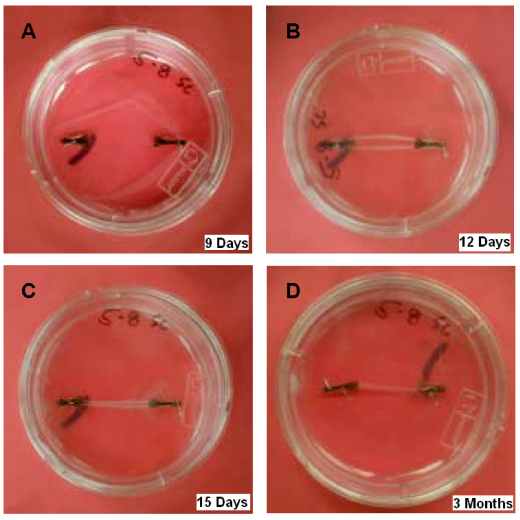
Different stages in the development of my colleague Sarah's engineered tendon constructs.
Our work involves mathematical and computational models of the processes of tissue growth and remodelling, in particular tissue engineered tendon, through mathematical modelling in a macroscopic continuum setting, and tissue culture. These models are motivated and validated by our controlled experiments on invitro engineered tissue. Morphogenesis is currently beyond the scope of this body of work.
A continuum treatment of growth in biological tissue
The ideas that follow are sufficiently general. They are applicable to soft and hard tissue involving multiple species, and the formulation can be applied to a specific tissue as our body of interest. In this treatment, we consider growth of biological tissue at a macroscopic scale. At this scale, the formulation though motivated by cellular, sub-cellular or molecular processes, does not explicitly model processes at this fine scale.
During the mathematical treatment of such phenomena, a variety of enhancements to standard continuum mechanics machinery are required to handle the complexity in the system now presented. We are now presented with,
- An open system with respect to mass
- Interacting and interconverting species
- Species diffusing with respect to a solid phase
- Mixture physics
Currently, we treat them in an elementary fashion, using source/sink terms that govern inter-conversion of species, and the mass fluxes that supply reactants and remove byproducts. The treatment is mathematical, and explicit incorporation of biochemical and cellular processes within our description will be carried out subsequently. Essential to the understanding of this description are the notions of the solid phase, the fluid phase, and the other precursors and byproducts of biochemical reactions. The solid phase is an anisotropic composite that is inhomogeneous at microscopic and macroscopic scales. The fluid, being mostly water, is modelled as compressible with a very large bulk modulus. The various constituents are assumed to diffuse through the solid phase. Virtually all biological tissue consists of a solid and fluid phase and can be treated in the context of mixture theory.
Some of the highlights of our treatment include:
- Multiple species undergoing transport, interconversion, mechanical and thermodynamic interactions
- Other species deform with the solid phase and diffuse with respect to it
- Fully compatible with mixture theory
- Detailed coupling of mechanics and mass balance
- Thermodynamic consistency
With that brief background out of the way, we now see how classical balance laws are enhanced by addition of these sources/sink and flux terms. Without really getting into the details, I am going to present relevant equations here. The terms that show up in the equations and figures have been described in slides 49 - 52 of this presentation. They have been written out for a species, in the reference configuration. As a final detour before I delve into the mathematics, it is beneficial to consider the continuum potato description of the system.
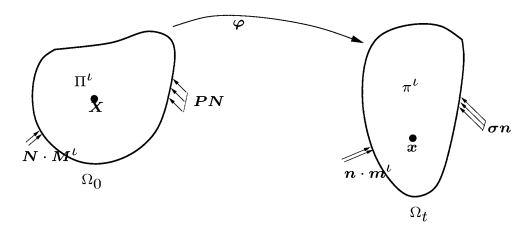
The continuum potato picture of things.
It is easiest to comprehend the equation for the balance of mass by considering the two terms on the right hand side individually. The first arises due to the existence of a source term for the species under consideration, and the second arises due to the existence of a flux. (The negative sign arises from the convention that an outward normal is positive. And an outward flux will tend to reduce the concentration of that species.)
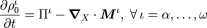
The balance of mass.
Similarly, we go on to see how linear momentum balance is affected by terms involving mass transport. In order to see the physical relevance, a material velocity, analogous to the flux in the balance of mass, relative to the solid is introduced. We then get the balance of linear momentum to be of the form,
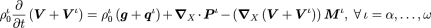
The balance of linear momentum.
Again, it is easiest to see how this relates to classical results when each of the terms on the right hand side are analysed separately. The first two, corresponding to the body force and partial stress respectively, are classical terms. The final term is an addition in momentum to the system due to the flux of the species.
Before we proceed, we realize a subtlety with respect to the kinematics of growth. We thus apply a suitable multiplicative decomposition of the deformation gradient into a growth tensor and an elastic deformation gradient. The split will be apparent in the figure below.
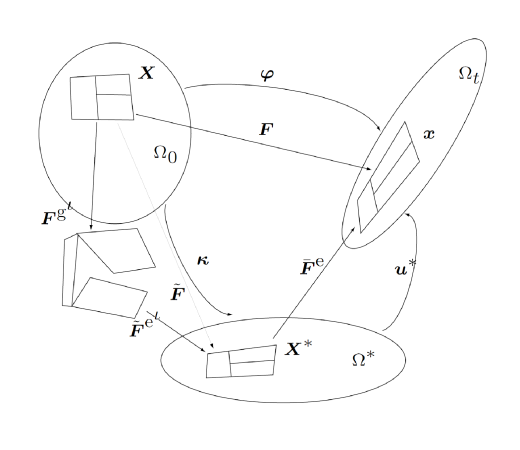
The continuum potato picture describing growth kinematics.
Proceeding in a similar manner to what was followed for balance of mass and momentum, the (first law of thermodynamics) balance of energy is written out.
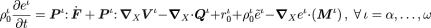
The balance of energy.
We recognize the terms on the right hand side to be the stress power terms, energy loss due to heat flux outwards, energy gain due to pointwise heat generation, energy gain due to internal energy inflow, and energy loss due to flux of species outwards. Finally, we write out the (second law of thermodynamics) entropy inequality, and combine it with the energy balance equation to get the dissipation inequality below.
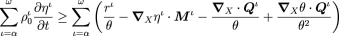
The dissipation inequality.
Assuming a suitable constitutive hypothesis for the stored energy (that it is a function of the elastic deformation gradient, the species density, and entropy) results in the following constitutive relations in accordance with the dissipation inequality.

Constitutive relations - 1.
The relations above are fairly standard and expected. The most interesting is the final one below.
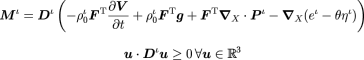
Constitutive relation - 2.
This relation describes how the flux of a given species relates to the different driving forces. It can be thought of as a product of a mobility and the driving forces due to various phenomena (inside the parenthesis). It is easy to imagine this in terms of a wet sponge. If the sponge is moved with an acceleration in a certain direction, the fluid it holds will be accelerated in the opposite direction. This is the first term, the driving force due to inertia. The second is plain to see. If the sponge is under the influence of a body force, say gravity, the driving force on the fluid will be along that direction. The next term is the stress gradient term (Darcy's law). If you squeeze the sponge to a certain stress state, the fluid it contains will be driven in a direction as indicated by that term. The final term can be shown to be the driving force arising from chemical potential.
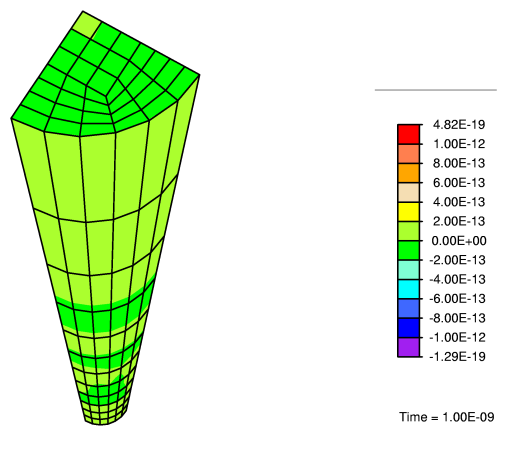
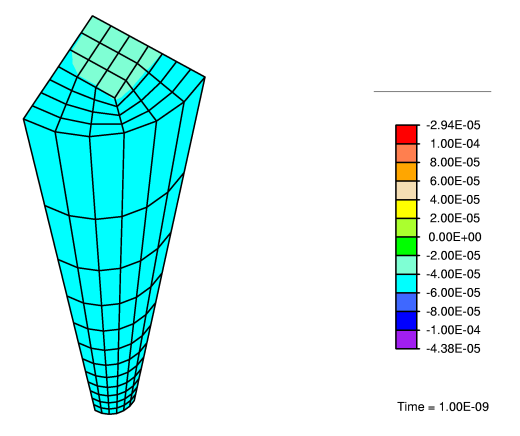
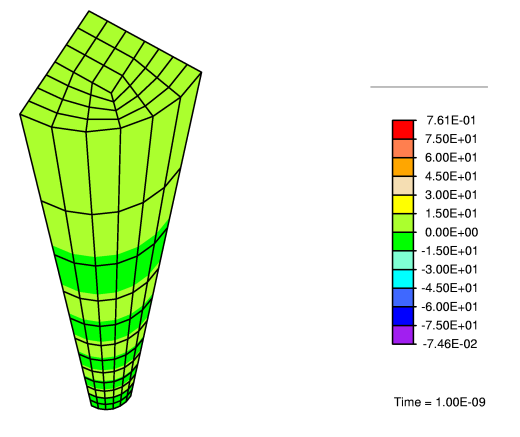
And finally, for a numerical example, we consider a system similar to our engineered construct soaked in a fluid bath. The dimensions of the cylinder and its properties are based on biological models. The problem considered is as shown in the picture below. The cylinder is stretched outwards in the 33 direction while all around its boundary, the mechanical conditions are traction free, and the fluid concetration is maintained a constant. Fluid is allowed to flux in and out of all surfaces.
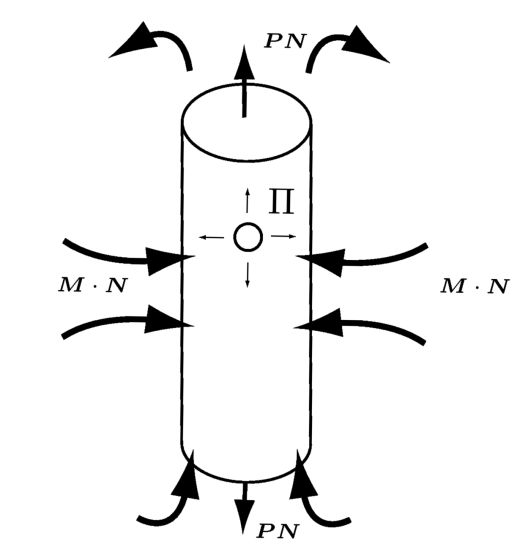
An image describing the numerical example.
In this biphasic model considered, the solid phase, collagen, is modelled using the worm-like chain model. The interstitial fluid phase, water, is modelled as a compressible fluid with large bulk modulus. Since we only have two phases, artificial sources for the fluid were considered using a simple first order law. The formulation above was reworked in weak form, and then resulted in a three dimensional finite element formulation which was implemented in FEAP.
In order to visualize the results of the computations, I have linked to a set of videos that show evolution of various fields with time. Clicking on the images below should link you to the corresponding video. The computations were carried out in FEAP and the videos from the plots were rendered using Imagemagick.
A continuum treatment of remodelling in biological tissue
(Will be populated when I have the time.)
Previous Research
(Will be populated when I have the time.)